#DIVULGACIÓN
DESDE EL ICN
DESDE EL ICN
• En particular, el Dr. Quevedo presentó la propuesta de la geometrotermodiámica, y la caracterizó como una “teoría efectiva”.

Investigador Titular C
Departamento de Gravitación y Teoría de Campos

Investigador Titular C
Departamento de Gravitación y Teoría de Campos



(Crédito: INSTAPUMA @VISITOR_FROM_PLANET_X)
Hernando Quevedo llegó a nuestro ciclo #FuturosICN con un propósito (o más bien, con una promesa): demostrarnos que es posible pensar en los fenómenos de la naturaleza, en términos de geometría. Y el nuestro es otro: mostrarte que estos caminos entre la física y las matemáticas pueden ser parte de tu modo de entender el Cosmos, ¡o incluso ser una alternativa para tu futuro como profesional!
Vamos pues a la introducción de Hernando Quevedo, investigador del Departamento de Gravitación y Campos del ICN, con el siguiente razonamiento: supongamos que tenemos un espacio dado y que en éste existen puntos; en torno a éstos existen vecindades: a cada punto le rodea un conjunto de otros puntos. Ahora bien, aunque un espacio sea curvo globalmente, en el orden de lo local, es decir, en la vecindad en torno a cada punto, el espacio es plano.
A este espacio localmente plano lo puedo dimensionar, o sea, darle dimensión, asignando para describirle un conjunto de números reales. Y en este espacio localmente plano, ya dimensionado con su “tejido” de números reales, a cada punto le puedo asignar, entonces, unas coordenadas: un conjunto de números reales para asignar su “identidad”: su diferencia, su caracterización dentro de ese espacio. Cada punto “coordinado” es en sí, distinto de otros que se encuentran en su vecindad. Esta diferenciación nos permite pensar en la noción de variedad diferencial. ¿Y ves? Ya estamos haciendo geometría.
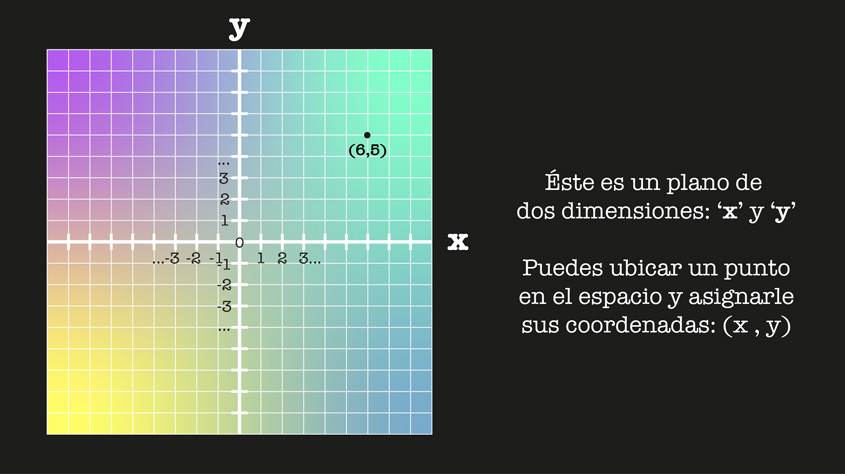
Recuerda el plano cartesiano que te enseñaron en la primaria...
Hernando Quevedo nos explica que, si tenemos dos puntos en un espacio dado, podemos definir la distancia entre ellos. La distancia entre un punto y otro punto en la vecindad puede describirse con una métrica, una matriz de números que nos permite determinar la diferencia entre un punto y otro: esta diferencia es su distancia. En la escuela nos enseñan a pensar en matrices de coordenadas de hasta tres dimensiones cuando nos enseñan los planos cartesianos.
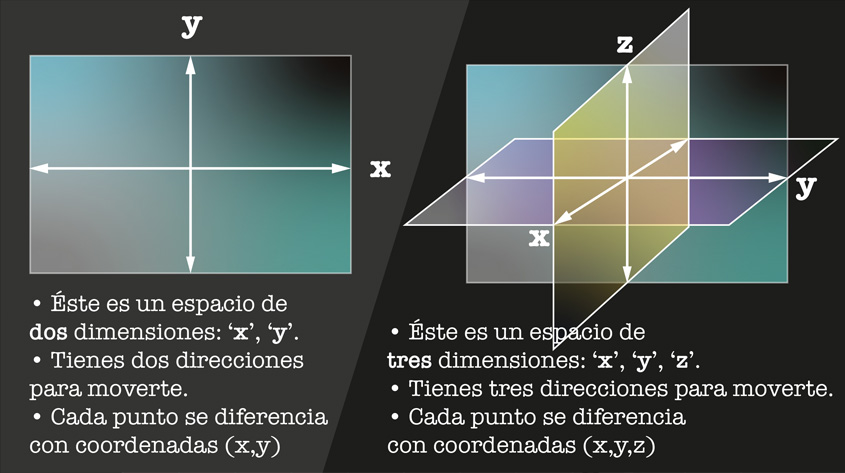
Los ejes ‘x’, ‘y’, ‘z’, representan las direcciones en las que podemos movernos en ese espacio. Cada una de estas letras nos habla, pues, de las dimensiones de nuestro espacio: la cantidad de direcciones en las que nos podemos mover es la cantidad de dimensiones a considerar.
Pero resulta que el universo, más allá de lo que perciben nuestros ojos, no es plano. Ni siquiera es tridimensional. Una métrica como la de Euclides, la geometría que nos enseñan en la escuela para pensar en espacios de una, dos o tres dimensiones, con sus matrices cartesianas, no da para comprender un universo de cuatro o más dimensiones… Necesitamos más que nuestra experiencia cotidiana.
Los objetos que vemos en la vida cotidiana tienen alto, ancho y profundidad: tienen tres dimensiones espaciales. Si todo lo que vemos parece tridimensional, ¿por qué los físicos dicen que el universo tiene más dimensiones?
Hernando Quevedo nos da, entonces, unas primeras ideas desde la geometría. Afirma que el instrumento matemático para comprender nuestro Universo es un Tensor de Curvatura: éste nos permite medir la diferencia entre dos puntos, pero en un espacio con cualquier número de dimensiones. Un tensor de curvatura nos permite pensar en objetos con múltiples números de dimensiones: justo como los físicos afirman que es nuestro Universo.
Probablemente no podemos visualizar (por ejemplo, dibujando) un objeto de cuatro dimensiones, sin vernos obligados a reducirlo representacionalmente a tres. Nuestro mundo y nuestra mente parecieran estar constreñidas a solo tres dimensiones espaciales.

Un hipercubo o teseracto es un objeto cuatridimensional, pero sus dimensiones en nuestras representaciones gráficas están constreñidas a solo tres. ¿Acaso ves algo que no sea un cubo raro dentro de otro cubo? ¿Podrías imaginar un objeto o espacio de 4 o más dimensiones? (Crédito: https://www.epsilones.com/paginas/0-bestiario/bestiario-hipercubo-tetradim.html)
Sin embargo, matemáticamente, es posible romper con este límite: con tensores, nos dice Hernando, podemos pensar en eso o en un número ilimitado de dimensiones. La imaginación, sustentada en la experiencia y la intuición, se extiende de formas sorprendentes cuando tiene este recurso matemático. Los tensores de curvatura son sin duda como el LSD de la geometría: nos ayudan a expandir nuestra imaginación dimensional.
Con el tensor de curvatura se puede describir matemáticamente lo que entendemos de manera intuitiva como un plano: cuando se describe un espacio plano, el tensor de curvatura es igual a cero (así es, lo que es plano, ¡no tiene nada de curvo! Por eso todas las componentes del tensor de curvatura son igual a cero). Pero si queremos describir algo que no es plano, el tensor de curvatura también nos sirve: alguna de sus componentes va a ser distinta a cero.
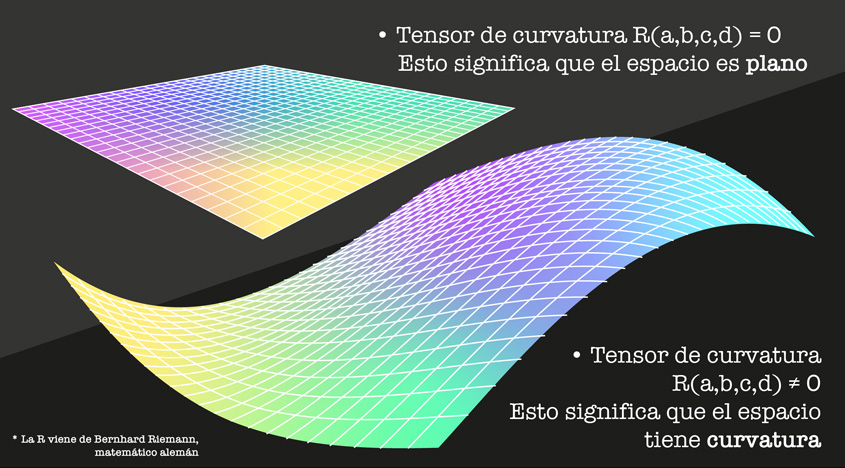
Desde la perspectiva de la curvatura de un espacio, hay entonces solo dos tipos de variedades diferenciales: Si el tensor de curvatura es cero, le llamamos plano. Si algunas de las componentes del tensor en cambio son diferentes de cero, le llamamos variedad curva.
Mediante ciertas combinaciones de las componentes del Tensor de Curvatura se puede construir lo que se conoce como el tensor de Einstein. Éste depende únicamente de la curvatura y de la métrica del espacio del que estemos hablando, es decir, es solo geometría.
Lo que hizo Einstein en 1915 fue proponernos un chispazo de imaginación: estableció una igualdad entre su tensor, que retoma componentes del tensor de curvatura de un espacio geométrico, matemático, y un tensor energía-momento, en el que se introducen cantidades que entendemos como físicas: por ejemplo, la masa, las densidades, las tensiones, las presiones…
El tensor energía – momento, nos cuenta Quevedo, depende de lo que quiera describir físicamente: por ejemplo, un gas ideal, un fluido perfecto, un campo electromagnético. Cualquier cosa con un sentido físico, se puede construir un tensor momento-energía correspondiente.
Pero aquí algo anda raro. ¿Cómo se puede igualar algo geométrico con algo físico? Todavía nos queda saber cómo, en esta ecuación, Einstein igualó peras curvas geométricas, matemáticas, con manzanas físicas. Nos pregunta Hernando: “¿cómo comparar por ejemplo algo que se mide en metros (del lado geométrico), con alguna magnitud física (por ejemplo, en kilogramos)?”. Así, de forma directa, no se puede. Para hacerlo, debo poner ambos términos en las mismas dimensiones físicas.
Si de un lado de la comparación, de la igualdad, tengo geometría (que no tiene restricciones fuera de su marco matemático) y del otro lado de la igualdad tengo física, debo considerar las restricciones, ¡que vaya que existen!, en el Cosmos, las constantes universales: la velocidad de la luz y de la gravedad. Este componente del lado de la física, que considera las restricciones que hay para todo fenómeno en el Cosmos, es lo que conocemos como la Constante de Einstein: 8πG/c4, donde 'G' es la constante gravitacional de la Teoría de Newton y 'c', la velocidad de la luz.
La igualdad entre, por un lado, un tensor de Einstein que recoge componentes desde la geometría, y por otro, un elemento que recoge las constantes universales de la gravedad y la velocidad de la luz, aunado a cantidades del fenómeno de la física que queramos estudiar, representado mediante un tensor-energía-momento es, de acuerdo con Hernando Quevedo, el legado más importante de la Teoría de Einstein.
Tensor de Einstein (con componentes del tensor de curvatura) [Geometría] =
Constante de Einstein y Tensor energía-momento [Física]
Ésta, nos reitera Hernando, es la idea más profunda y bella que nos presentaron las ecuaciones de Einstein.
El doctor Quevedo entonces nos presenta algunos ejemplos concretos en los que echamos mano de los tensores, desde la geometría, para dilucidar fenómenos de la física.
Ejemplo 1. Relatividad especial y la simetría entre marcos de referencia
Como decíamos antes, en nuestro día a día pareciera que vivimos en un universo tridimensional: tres dimensiones espaciales (ancho ‘x’, alto ‘y’, y profundo ‘z’). Pero resulta que también tenemos una dimensión temporal ‘t’: el paso del tiempo. Nada ocurre fuera de este conjunto dimensional. De allí que hablemos de que el Universo existe en una entidad única, que llamamos el espacio-tiempo.
A esta variedad diferencial de cuatro dimensiones se le conoce como el espacio-tiempo de Minkowski. Y ¡zas!, sí, son cuatro. Esto significa que nuestra geometría euclidiana no nos alcanza… Necesitamos echar mano de tensores de curvatura para pensar en algo así.
Al pensar el espacio-tiempo mediante la relación entre geometría y física, esto es, usar tensores para describir la distancia entre dos puntos en el espacio-tiempo, Einstein pudo postular su teoría especial de la relatividad, con la cual podemos ver que tanto el espacio como el tiempo en el que “habita” un marco de referencia (por ejemplo, una nave espacial), dependerá desde dónde lo observemos.
En este caso estamos hablando de una teoría especial, porque un espacio-tiempo de Minkowski resuelve las ecuaciones de Einstein de tal manera que los tensores de curvatura y el tensor de Einstein, y por lo tanto el tensor energía-momento, son cero: es decir, este espacio-tiempo es plano. Es un caso “ideal”, si lo queremos ver así, porque este espacio-tiempo no cuenta con curvatura geométrica ni fenomenología física alguna.
En este espacio-tiempo ideal, imaginemos lo siguiente. Si desde nuestro marco de referencia, por ejemplo, desde nuestro planeta, marco que consideramos fijo (pues estamos “allí, en el planeta”) observamos una nave espacial (otro marco), que se encuentra en movimiento con relación al nuestro, podremos ver que tanto el espacio como el tiempo de la nave, que está en movimiento con relación a nosotros, se está “alterando”: su tiempo y el espacio se alteran. Esta alteración dependerá de cuán rápido se mueva esa nave con relación a nuestro marco, que consideramos fijo (pues recuerda, estamos allí, sobre el planeta). Pero hay una cuestión: resulta que los que estén en ese otro marco de referencia, en la nave, están “allí”, es decir, para ellos su marco es el fijo, y nosotros somos los que nos estamos moviendo con respecto a ellos. Para ellos, nuestro planeta y nosotros somos los que nos movemos. Por ello, verán que nuestro espacio-tiempo se ve alterado, mientras que el suyo permanece normal, y esta alteración que ellos observan en el nuestro espacio-tiempo será más grande en tanto nosotros nos movamos más rápido en relación con ellos.
Este fenómeno físico, la alteración del espacio-tiempo dependiendo del marco de referencia, que ha sido comprobado muchas veces y que debemos considerar para que funcionen muchos de nuestros instrumentos tecnológicos actuales, vino a la mente de Einstein al pensar el problema en términos de geometría del espacio-tiempo, mediante el uso de tensores que lo presentaban como un plano.
Ahora bien, algo importante a notar con este ejemplo ilustrativo es que hay una simetría, una invariancia entre lo que observan ambos marcos de referencia: no hay un marco evidentemente fijo, y el otro evidentemente en movimiento. Ambos estados (‘fijo’ y ‘en movimiento’) dependen del propio lugar desde donde se hace la observación. Es decir, hay una simetría en la perspectiva física de todos los marcos de referencia. Esta simetría se puede comprender, en la teoría especial, con las llamadas invariancias de Lorentz.
Ejemplo 2: La teoría general de la relatividad de Einstein: gravedad
Pero también puede haber soluciones a las ecuaciones de Einstein, en las que el tensor de curvatura no resulta en cero. Es decir, estamos hablando de un espacio-tiempo donde hay curvatura. En esta propuesta de solución a las ecuaciones de Einstein, pensemos en una variedad diferencial en la que el tensor de curvatura es distinto de cero, pero el tensor de Einstein y por tanto el tensor energía-momento, sí resulta en cero. Esto quiere decir que en esta variedad diferencial no hay más componentes de la física que la propia geometría del espacio-tiempo.
La curvatura, infirió Einstein, en esta solución, nos describe la interacción gravitacional. O lo que es lo mismo: una estructuración geométrica curva del espacio-tiempo nos produce un fenómeno físico: la gravedad.

Ejemplo 3: Teoría general de la relatividad respecto a la Evolución del Universo
Todavía hay una tercera solución, en la que el tensor de la curvatura es diferente de cero, pero además el tensor de Einstein (que retoma los componentes del tensor de curvatura) se iguala al tensor de energía – momento que ahora contiene la presión y la densidad del universo y que, en efecto, es diferente de cero (pues el Cosmos tiene una densidad y tiene una presión).
Con esta solución de las ecuaciones de Einstein, en la que el tensor de curvatura es distinto de cero (es decir, hay una curvatura en el espacio-tiempo) y en la que el tensor de Einstein, que se iguala con el tensor energía - momento que considera las cantidades físicas relacionadas con la presión y la densidad del Universo es también distinto de cero (pues el universo tiene una presión y densidad físicas), se puede describir la evolución del Universo. Hay progresiones de cambio en el tiempo, para la presión y la densidad del Universo, mientras éste se expande.

Representación de la evolución del Universo en expansión - Da click sobre la imagen para agrandar
(Crédito: https://www.astromia.com/universo/evolucion.htm)
En este último par de soluciones, lo importante a resaltar es que toda la teoría es invariante con respecto a cambios de coordenadas, esto es, hay una simetría, lo cual significa que la física del campo gravitacional no depende de las coordenadas que se usen para describirla.
Hernando nos cuenta entonces que la teoría de Einstein tiene los siguientes ingredientes:
- Una métrica, para comprender la noción de distancia entre dos puntos en el espacio-tiempo
- La curvatura, que se deriva a partir de la métrica, y que nos permite comprender las interacciones gravitacionales.
- La simetría para poder construir la teoría. En el caso especial, es la invariancia de Lorentz; en el caso de la teoría general de la relatividad, la métrica no cambia, aunque se cambien las coordenadas.
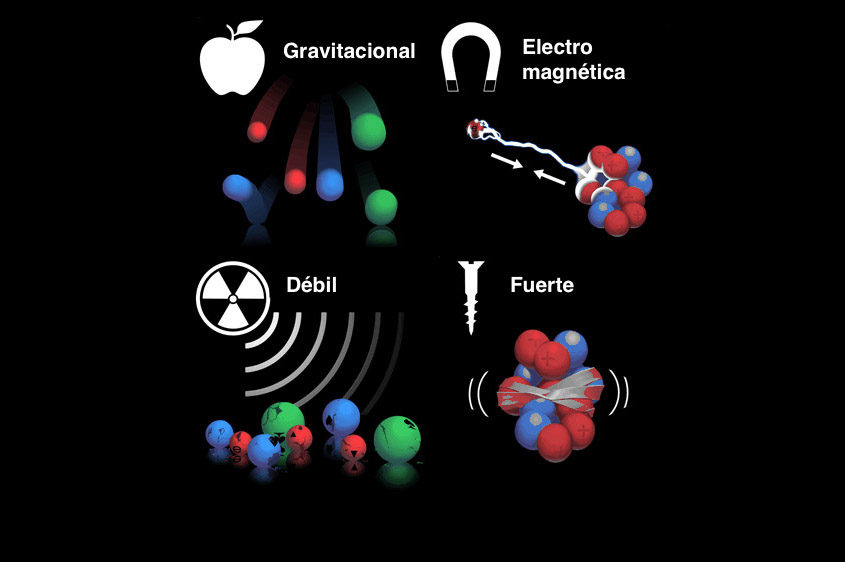
Pero Hernando Quevedo nos explica que además de la fuerza de gravedad, que nos da cuenta de fenómenos del orden de interacciones de magnitudes planetarias, galácticas y cósmicas, también es posible hacer representaciones geométricas para entender las otras fuerzas en el orden de la física de lo cuántico, que se dan en magnitudes de lo subatómico: las interacciones débiles, las electromagnéticas y fuertes.
Ejemplo 4: explicar tres fuerzas fundamentales: electromagnética, débil y fuerte
Como vimos, la interacción gravitacional tiene dos variedades diferenciales geométricas posibles: curvo o no curvo. En contraste, cada una de las otras tres fuerzas de la naturaleza tiene un número mayor de variedades diferenciales geométricas posibles.
Hernando nos explica que, para describir las interacciones electromagnética, débil y fuerte desde la geometría, se puede recuperar de ésta la noción de haces fibrados, que a su vez retoma la noción de plano y recta geométricas, considerando las cuatro dimensiones del espacio-tiempo como el plano que les contiene, más las dimensiones de la “fibra” que caracteriza a cada fuerza.
Quevedo nos cuenta brevemente sobre las teorías de Yang y Mills para hacernos ver esta relación sorprendente: mediante consideraciones matemáticas del orden geométrico, podemos comprender las interacciones físicas del electromagnetismo, la fuerza débil y la fuerza fuerte, y cómo se siguen manteniendo invariancias en cada una de ellas. Para ilustrar el punto, Hernando se centra en exponer cómo los haces fibrados en geometría pueden describir la fuerza electromagnética, un fenómeno físico que vivimos cotidianamente.
Ejemplo 5: Explicar las cuatro fuerzas fundamentales con un mismo instrumental de la geometría
Hernando Quevedo también nos expone cómo otra noción geométrica denominada “mapeo de encajamiento”, donde una variedad diferencial “se encaja” en otra variedad diferencial, tiene su uso en la física teórica, particularmente en la famosa teoría de cuerdas.
Esta teoría retoma el instrumental de la geometría diferencial, para describir con un solo recurso teórico y geométrico (las cuerdas y sus modalidades de vibración) las cuatro fuerzas de la naturaleza. Esta “teoría del Todo” es como el Santo Grial de la física contemporánea. La Teoría de Cuerdas es una candidata que intenta pelear su lugar como tal.
En un detalle interesante, Hernando Quevedo nos comenta que el vaivén entre geometría y física no es unidireccional: hemos visto que la geometría va “delante” de la física al darle elementos para desarrollar sus teorías. Pero en el caso de la teoría de cuerdas, es la física la que alimentó a las temáticas de la geometría diferencial. Por querer explicar las cuatro interacciones de la naturaleza con un mismo instrumental matemático, y ser una “Teoría del todo”, los físicos promovieron nuevos caminos para la geometría diferencial. La intención de unificar las fuerzas desde la física crea nuevos caminos para las matemáticas, y mantienen así un vaivén creativo que se sostiene en el presente.
Hernando Quevedo ya nos mostró que las cuatro fuerzas de la naturaleza se pueden explicar geométricamente. Podemos abordarlas a cada una por separado, como se ha hecho por un lado con la gravedad y por otro con las otras tres fuerzas (electromagnética, débil y fuerte), o podemos tratar de unificarlas como una manifestación de un mismo fenómeno físico mediante la teoría de cuerdas y su correspondiente aproximación geométrica. Mostrar las partículas relacionadas con cada fuerza.
Pero nuestro investigador lanza una provocación: ¿qué sucedería si tomamos todas las fuerzas, es decir, todas las partículas involucradas en la manifestación de estas interacciones, y en vez de describirlas una por una, las tratamos de describir como un conjunto, un sistema que contiene un número enorme de ellas (del orden de 1023), en el cual considero todas las interacciones que hay?
Sabemos que cuando tenemos un número así de partículas, es imposible describir a cada una de ellas individualmente, y mucho menos las continuas interacciones entre sí. Para este tipo de conjunto usamos las aproximaciones de la termodinámica en física: tomamos un promedio de las fuerzas entre todas esas partículas. Hernando indica: “ya no hay fuerzas en el sentido estricto de la palabra. Hay variables termodinámicas, como lo son la temperatura, el volumen o la presión”.
Quevedo retoma la noción de punto en un plano que satisfacen las ecuaciones de un gas ideal, un espacio en equilibrio, y la noción de “mapeo de encajamiento” que habla de un espacio embebido en otro. Así, este espacio en equilibrio está contenido en otro espacio, el llamado “espacio de fase”.
Entonces presenta Hernando Quevedo su propuesta de formalismo: la geometrotermodinámica. Mediante las consideraciones de la física de la termodinámica, es posible plantear una representación geométrica de un conjunto enorme de partículas en un gas. Por ejemplo, explica, el gas ideal tiene su representación geométrica en un espacio plano en dos dimensiones (su tensor de curvatura por lo tanto es cero). Un gas Van der Waals sí tiene interacción termodinámica es un espacio de dos dimensiones, pero con cierta curvatura, y en el cual hay puntos o “agujeros” que representan transiciones de fase.
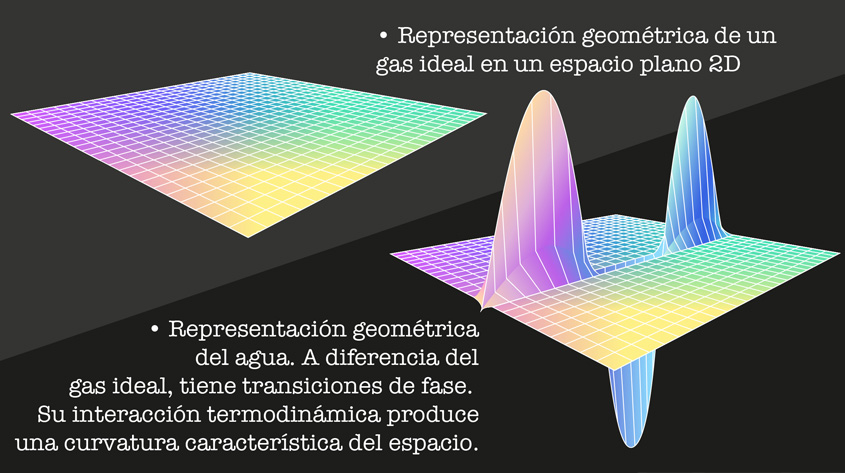
Si hay una reacción química, una combinación de muchos componentes, es posible describirla en un espacio de dos dimensiones, donde la reacción consiste en pasar de un punto, un estado de equilibrio, a otro estado de equilibrio, a través de muchos otros estados de equilibrio. La geometrotermodinámica se puede aplicar también para representar diferentes distribuciones estadísticas usadas en física de plasmas, en el caso de los agujeros negros, y para describir el universo, procedimiento que aun está en construcción.
La idea que propone Hernando Quevedo desde el ICN se resume así: donde quiera que exista un sistema termodinámico, podemos introducir la geometrotermodinámica y encontrar su representación geométrica.
La diferencia en las aproximaciones de la Teoría de Cuerdas y la Geometrotermodinámica, explica Hernando, radica en que mientras que la primera busca ser una teoría completa, la segunda busca ser una teoría efectiva.
A Hernando Quevedo, a su propuesta sistémica y al vaivén entre la física y la geometría les queda todavía mucho por entretejer para explicarnos, al menos de forma teórica, los fenómenos de la naturaleza. De allí que puedas unirte, para hacer de su propuesta parte de tu propio vaivén personal.
También puedes ver la charla completa sobre este tema aquí:
Puedes ver las charlas del primer semestre de 2022 en los siguientes links:
- • Desde los átomos a las estrellas
Charla con el Dr. Fabio de Colle (ICN-UNAM). Febrero 25, 2022 - • Dosimetría de la radiación ionizante en aplicaciones en la medicina
Charla con la Dra. Isabel Gamboa (ICN-UNAM).Marzo 25, 2022 - • Más rápido que la luz
Charla con el Dr. Miguel Alcubierre (ICN-UNAM). Mayo 27, 2022 - • Átomos y luz para medir. ¿Qué? ¿Cómo? ¿Por qué?
Charla con el Dr. José Jiménez (ICN-UNAM). Junio 24, 2022


